রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র
এই টিউটোরিয়ালটি শেষে -
রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র ব্যাখ্যা করতে পারা যাবে।
রম্বসের ক্ষেত্রফল বর্ণনা করতে পারা যাবে।
রম্বসের ক্ষেত্রফলের সূত্র প্রতিপাদন করতে পারা যাবে।
রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র বিভিন্নভাবে উদ্ভাবন করতে পারা যাবে।
ত্রিকোণমিতি ব্যবহার করে কিভাবে রম্বসের ক্ষেত্রফল সূত্র প্রতিপাদন করা যায় তা বিশ্লেষণ করতে পারা যাবে।
রম্বসের ক্ষেত্রফল
চতুর্ভুজের চারটি বাহুর দৈর্ঘ্য সমান হলে তাকে রম্বস বলে। রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র প্রতিপাদন করার আগে রম্বসের ক্ষেত্রফল কি তা আগে জানা দরকার। রম্বসের বাহু চারটি দ্বারা বেষ্টিত পৃষ্ঠতলকে রম্বসের ক্ষেত্রফল বলে। অন্যভাবে বলা যায়, রম্বসের চারটি বাহু দ্বারা আবদ্ধ তল বা ক্ষেত্রকে রম্বসের ক্ষেত্রফল বলে।
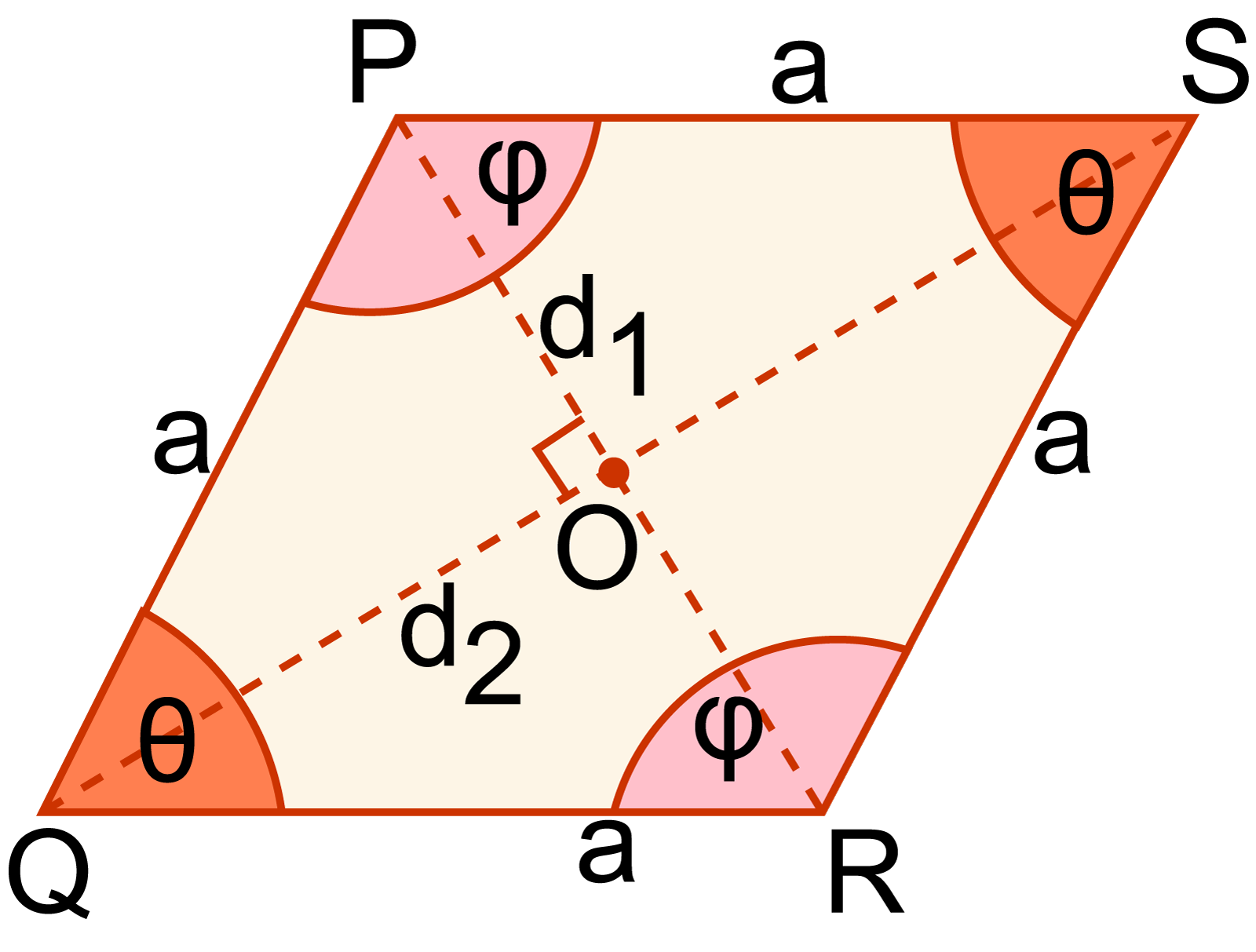
রম্বস ক্ষেত্রের তল বা পৃষ্ঠতল যাই বলা হোক না কেন, এই তল সবসময়ই একটি সমতল। এই সমতলের ক্ষেত্রফল নির্ণয়ের সূত্রই রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র বলে অভিহিত। রম্বসের বিপরীত কোণগুলো পরস্পর সমান। তবে রম্বসের কোণ হ্রাস-বৃদ্ধি হলে এর ক্ষেত্রফলেরও পরিবর্তন ঘটে। তাছাড়া, এর কর্ণ দুইটি একে অপরকে সমকোণে সমদ্বিখণ্ডিত করে।
আবার, রম্বসের যেকোনো বাহুর সংলগ্ন কোণ দুইটির সমষ্টি দুই সমকোণ বা ১৮০০। রম্বসের যেকোনো কর্ণ রম্বসকে দুইটি সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজে বিভক্ত করে।
আবার রম্বসের উভয় কর্ণ একত্রে রম্বসকে সমান ক্ষেত্রফল বিশিষ্ট চারটি সর্বসম ত্রিভুজে বিভক্ত করে। রম্বস হলো বিশেষ ধরণের একটি সামান্তরিক। তাই সামান্তরিকের ক্ষেত্রফলের সূত্র রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র হিসাবে প্রয়োগ করা যায়।
রম্বসের ক্ষেত্রফলের সূত্র
রম্বসের চারটি বাহু দ্বারা পরিবেষ্টিত তল হলো রম্বসের ক্ষেত্রফল। রম্বসের ক্ষেত্রফল বিভিন্নভাবে পরিমাপ করা যেতে পারে। তবে রম্বসের ক্ষেত্রফল নির্ণয়ের আগে রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র কি তা জানা দরকার।
সাধারণত যেসব উপায়ে রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র প্রতিপাদন করা যায়, তা নিম্নরূপঃ
- ভূমি ও উচ্চতার ভিত্তিতে রম্বসের ক্ষেত্রফল
- ভূমি ও শীর্ষকোণের ভিত্তিতে রম্বসের ক্ষেত্রফল
- উচ্চতা ও শীর্ষকোণের ভিত্তিতে রম্বসের ক্ষেত্রফল
- কর্ণদ্বয়ের ভিত্তিতে রম্বসের ক্ষেত্রফল
- অন্তর্লিখিত বৃত্তের ভিত্তিতে রম্বসের ক্ষেত্রফল
ভূমি ও উচ্চতার ভিত্তিতে রম্বসের ক্ষেত্রফল
রম্বসের কোনো শীর্ষবিন্দু থেকে যে বাহুর উপর লম্ব আঁকা হয়, ঐ বাহুকে রম্বসের ভূমি বলে। আর অঙ্কিত লম্বটিকে রম্বসের উচ্চতা বলে। একটি রম্বসের ভূমি ও উচ্চতার ভিত্তিতে কিভাবে রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র প্রতিপাদন করা যায় তা নিচে দেখানো হলোঃ
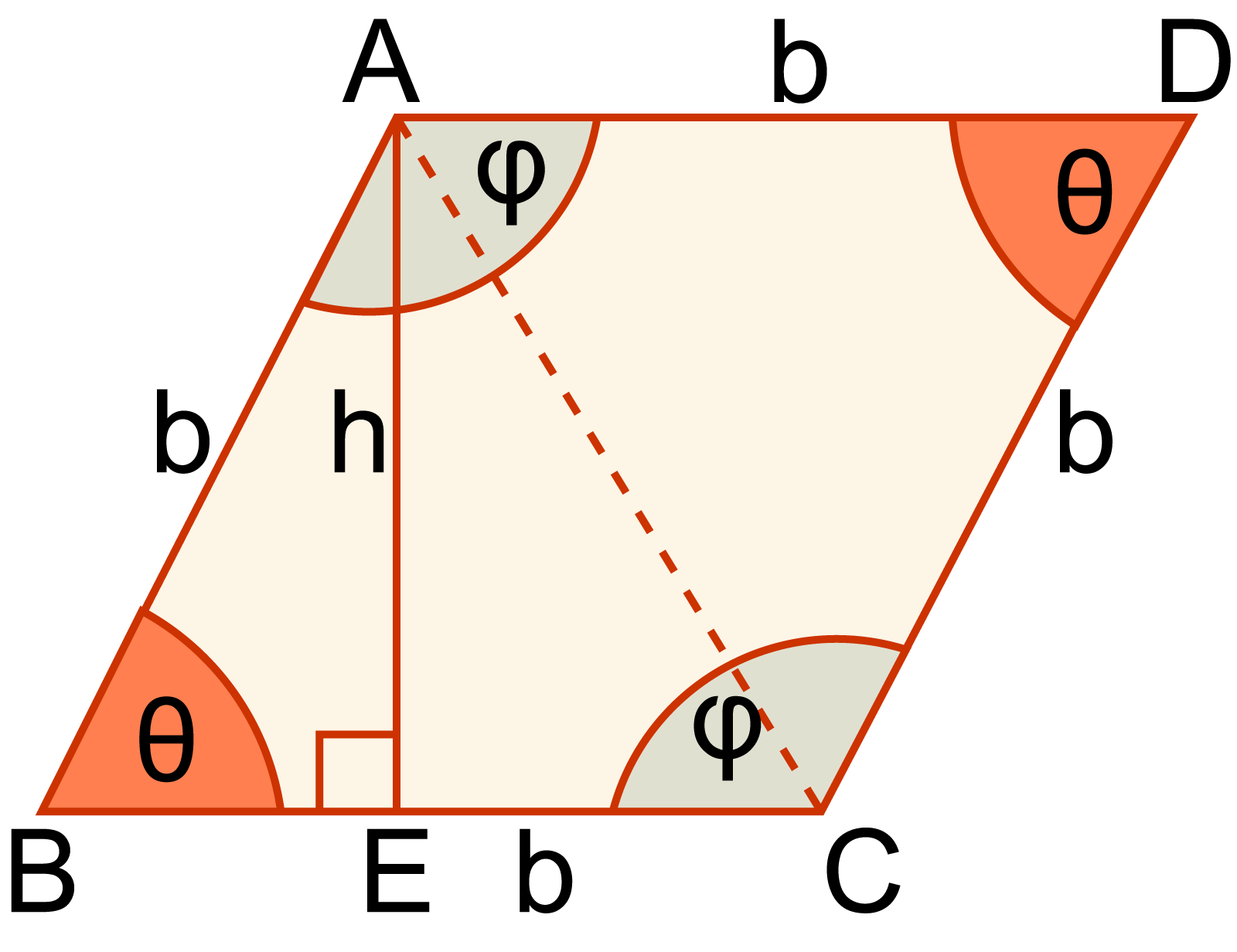
মনে করি, ABCD রম্বসের AB = BC = CD = DA = b.
AE⊥BC আঁকি যেখানে AE = h. আবার, AC কর্ণ আঁকি - যা রম্বসকে দুইটি ত্রিভুজে বিভক্ত করে।
এখন, △ABC ও △ADC -এ
AB = AD,
BC = CD এবং
AC = AC
∴ △ABC ≅ △ADC
ABCD রম্বসের ক্ষেত্রফল △ABC ও △ADC ক্ষেত্রফলদ্বয়ের সমষ্টির সমান। অর্থাৎ,
◇ABCD = △ABC+ △ADC
বা, ◇ABCD = △ABC+ △ABC [∵ △ABC ≅ △ADC]
বা, ◇ABCD = 2△ABC
বা, ◇ABCD = 2 × 12 × ভুমি × উচ্চতা
∴ ◇ABCD = ভুমি × উচ্চতা
রম্বসের ক্ষেত্রফল =(ভূমি × উচ্চতা) বর্গ একক।
রম্বসের ভূমি b একক এবং উচ্চতা h একক হলে,
রম্বসের ক্ষেত্রফল =(ভূমি × উচ্চতা) বর্গ একক। অর্থাৎ,
রম্বসের ক্ষেত্রফল =(b × h) বর্গ একক।
ভূমি ও শীর্ষকোণের ভিত্তিতে রম্বসের ক্ষেত্রফল
রম্বসের কোণ চারটি এবং প্রতিজোড়া বিপরীত কোণ দুইটি পরস্পর সমান। আর এই কোণগুলোর প্রত্যেকটিকে এক-একটি শীর্ষকোণ বলে। আর শীর্ষকোণ থেকে যে বাহুর উপর লম্ব অঙ্কন করা হয় ঐ বাহু রম্বসের ভূমি বলে পরিচিত। একটি রম্বসের ভূমি ও শীর্ষকোণের ভিত্তিতে রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র প্রতিপাদন করে নিচে দেখানো হলোঃ
মনে করি, PQRS রম্বসের PQ=QR=RS=PS=a.
P বিন্দু থেকে QR এর উপর PM লম্ব আঁকি। ফলে ∠PMQ=900 যেখানে PM=h. আবার, AC কর্ণ রম্বসকে △ PQR এবং △PSR দুইটি ত্রিভুজে বিভক্ত করে।
এখন, △PQR ও △PSR -এ
PQ = PS,
QR = RS, এবং
অন্তর্ভুক্ত ∠PQR = অন্তর্ভুক্ত ∠PSR
∴ △PQR ≅ △PSR
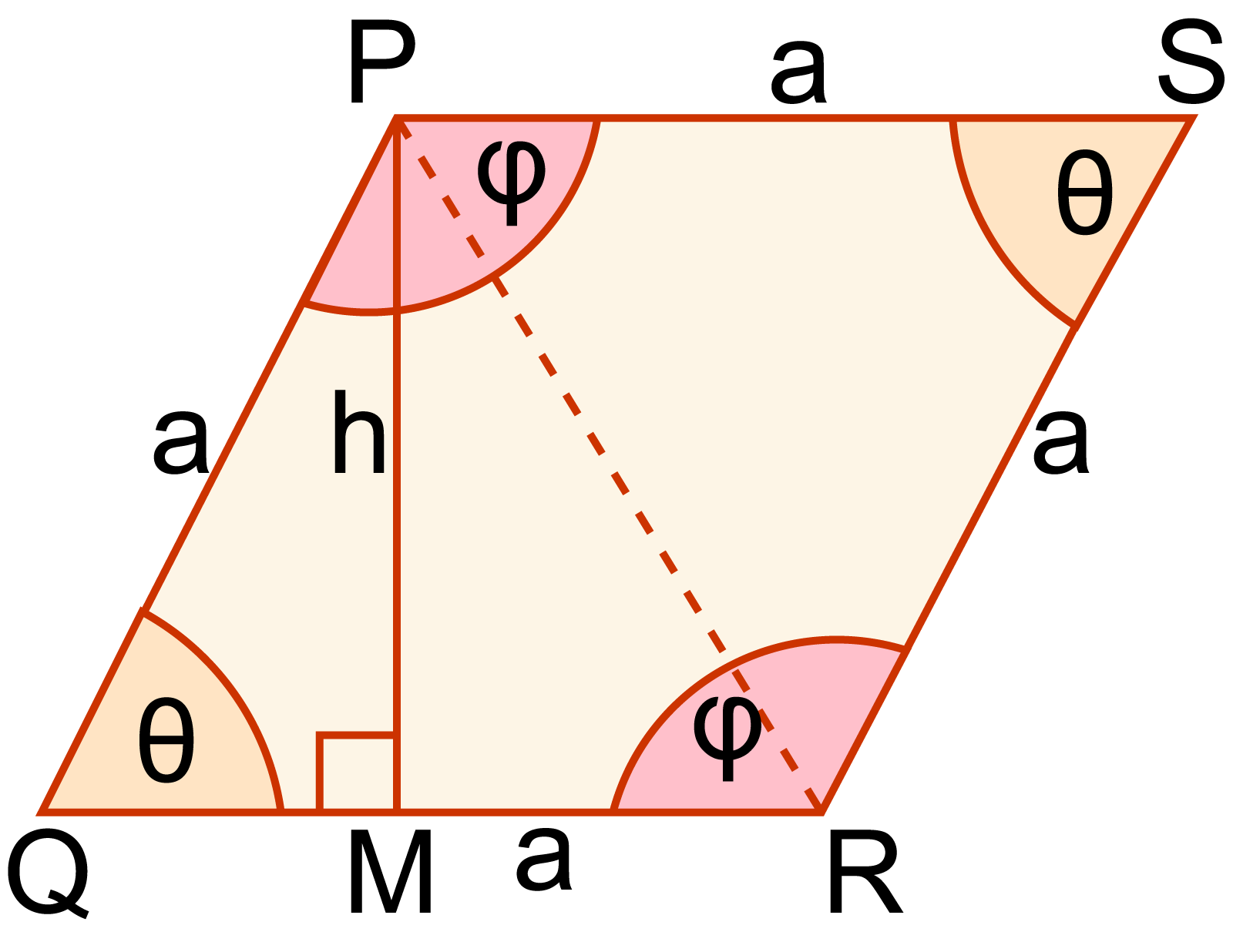
সমকোণী △ PQM -এ
sinθ = PMPQ
বা, sinθ = ha
∴ h = asinθ ...... (1)
PQRS রম্বসের ক্ষেত্রফল △PQR ও △PSR ক্ষেত্রফলদ্বয়ের সমষ্টির সমান। অর্থাৎ,
◇PQRS = △PQR + △PSR
বা, ◇PQRS = △PQR + △PQR [∵ △PQR ≅ △PSR]
বা, ◇PQRS = 2 × △PQR
বা, ◇PQRS = 2 × 12 × ভুমি × উচ্চতা
বা, ◇PQRS = ah
বা, ◇PQRS = aasinθ [∵ h = asinθ (1) নং হতে ]
∴ ◇PQRS = a2sinθ
অনুরূপভাবে প্রমাণ করা যায় যে,
◇ PQRS = a2sinφ
∴ রম্বসের ক্ষেত্রফল = a2sinθ বর্গ একক। অথবা,
রম্বসের ক্ষেত্রফল = a2sinφ বর্গ একক।
রম্বসের বাহুর দৈর্ঘ্য a একক এবং সন্নিহিত কোণদ্বয় θ ও φ হলে,
রম্বসের ক্ষেত্রফল = a2sinθ বর্গ একক।
রম্বসের ক্ষেত্রফল = a2sinφ বর্গ একক।
উচ্চতা ও শীর্ষকোণের ভিত্তিতে রম্বসের ক্ষেত্রফল
উচ্চতা ও শীর্ষকোণ ব্যবহার করে রম্বসের ক্ষেত্রফল সূত্র নির্ণয় করা যায়। একটি রম্বসের উচ্চতা ও শীর্ষকোণের ভিত্তিতে কিভাবে রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র প্রতিপাদন করা যায় তা নিচে দেখানো হলোঃ

মনে করি, PQRS রম্বসের বাহুর দৈর্ঘ্য a একক।
PM⊥QR আঁকি এবং মনেকরি, PM = h. আবার কর্ণ PR, রম্বসকে △PQR এবং △PSR দুইটি ত্রিভুজে বিভক্ত করে এবং ত্রিভুজ দুইটির অনুরূপ বাহু তিনটি পরস্পর সমান।
∴ △PQR ≅ △PSR
এখন, সমকোণী △ PQM -এ
sinθ = PMPQ
বা, sinθ = ha
∴ a = hsinθ ..... (2)
এখন, △PQR ও △PSR ত্রিভুজদ্বয়ের ক্ষেত্রফলদ্বয়ের সমষ্টি, PQRS রম্বসের ক্ষেত্রফলের সমান। অর্থাৎ,
◇PQRS = △PQR + △PSR
বা, ◇PQRS = △PQR + △PQR [∵ △PQR ≅ △PSR]
বা, ◇PQRS = 2△PQR
বা, ◇PQRS = 2 × 12
বা, ◇PQRS = 2 × 12 × ভুমি × উচ্চতা
বা, ◇PQRS = ভুমি × উচ্চতা
বা, ◇PQRS = ah
বা, ◇PQRS = hsinθ .h [∵ a = hsinθ (2) নং হতে]
∴ ◇PQRS = h2sinθ
একইভাবে প্রমাণ করা যায় যে,
◇PQRS = h2sinφ
∴ রম্বসের ক্ষেত্রফল = h2sinθ বর্গ একক। অথবা,
রম্বসের ক্ষেত্রফল = h2sinφ বর্গ একক।
রম্বসের বাহুর দৈর্ঘ্য a একক এবং সন্নিহিত কোণদ্বয় θ ও φ হলে,
রম্বসের ক্ষেত্রফল = h2sinθ বর্গ একক
রম্বসের ক্ষেত্রফল = h2sinφ বর্গ একক।
কর্ণদ্বয়ের ভিত্তিতে রম্বসের ক্ষেত্রফল
রম্বসের যেকোনো দুইটি বিপরীত শীর্ষবিন্দুর সংযোজক রেখাংশ হলো রম্বসের কর্ণ। এভাবে একটি রম্বসের দুইটি কর্ণ অঙ্কন করা যায়। কর্ণদ্বয় ব্যবহার করে রম্বসের ক্ষেত্রফল সূত্র নির্ণয় করা যায়। একটি রম্বসের কর্ণ দুইটির ভিত্তিতে কিভাবে রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র তৈরি করা যায় তা নিচে দেখানো হলোঃ
মনে করি, PQRS রম্বসের PQ = QR = RS = PS = a.
PR এবং QS কর্ণ দুইটি আঁকি যারা পরস্পরকে O বিন্দুতে ছেদ করে; যেখানে PR = d1 এবং QS = d2. আবার রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
∴ PO = d12, QO = d22, এবং ∠POQ = ৯০°.
এখন, △ POQ ও △ QOR -এ
∴ PQ = QR,
PO = RO এবং
QO = QO
∴ △POQ ≅ △QOR

অনুরূপভাবে প্রমাণ করা যায় যে,
△POQ ≅ △POS ≅ △ROS ≅ △QOR.
PQRS রম্বসের ক্ষেত্রফল △POQ, △QOR, △ROS ও △POS এই চারটি সর্বসম ত্রিভুজের ক্ষেত্রফলের সমষ্টির সমান। অর্থাৎ,
◇PQRS = △POQ + △QOR + △ROS + △POS
বা, ◇PQRS = △ POQ + △POQ + △POQ + △POQ
বা, ◇PQRS =4 × △POQ
বা, ◇PQRS = 4 × 12 × ভুমি × উচ্চতা [∵ ∠POQ = ৯০°]
বা, ◇PQRS = 4 × 12 ×d12 × d22
∴ ◇PQRS = 12 d1d2
রম্বসের কর্ণদ্বয়ের দৈর্ঘ্য d1 একক ও d2 একক হলে,
রম্বসের ক্ষেত্রফল = 12 d1d2 বর্গ একক
অন্তর্লিখিত বৃত্তের ভিত্তিতে রম্বসের ক্ষেত্রফল
অন্তর্লিখিত বৃত্তের ভিত্তিতে রম্বসের ক্ষেত্রফল নির্ণয়ের সূত্র কি তা জানার আগে রম্বসে অন্তর্লিখিত বৃত্ত কি - তা জানা দরকার। একটি রম্বসের প্রত্যেক বাহুকে স্পর্শ করে রম্বসের অভ্যন্তরে একটি বৃত্ত অঙ্কন করা হলে ঐ বৃত্তকে রম্বসে অন্তর্লিখিত বৃত্ত বলে। একটি বৃত্ত একটি রম্বসে অন্তর্লিখিত হলে তার ভিত্তিতে রম্বসের ক্ষেত্রফলের সূত্র কি তা প্রতিপাদন করে নিচে দেখানো হলোঃ
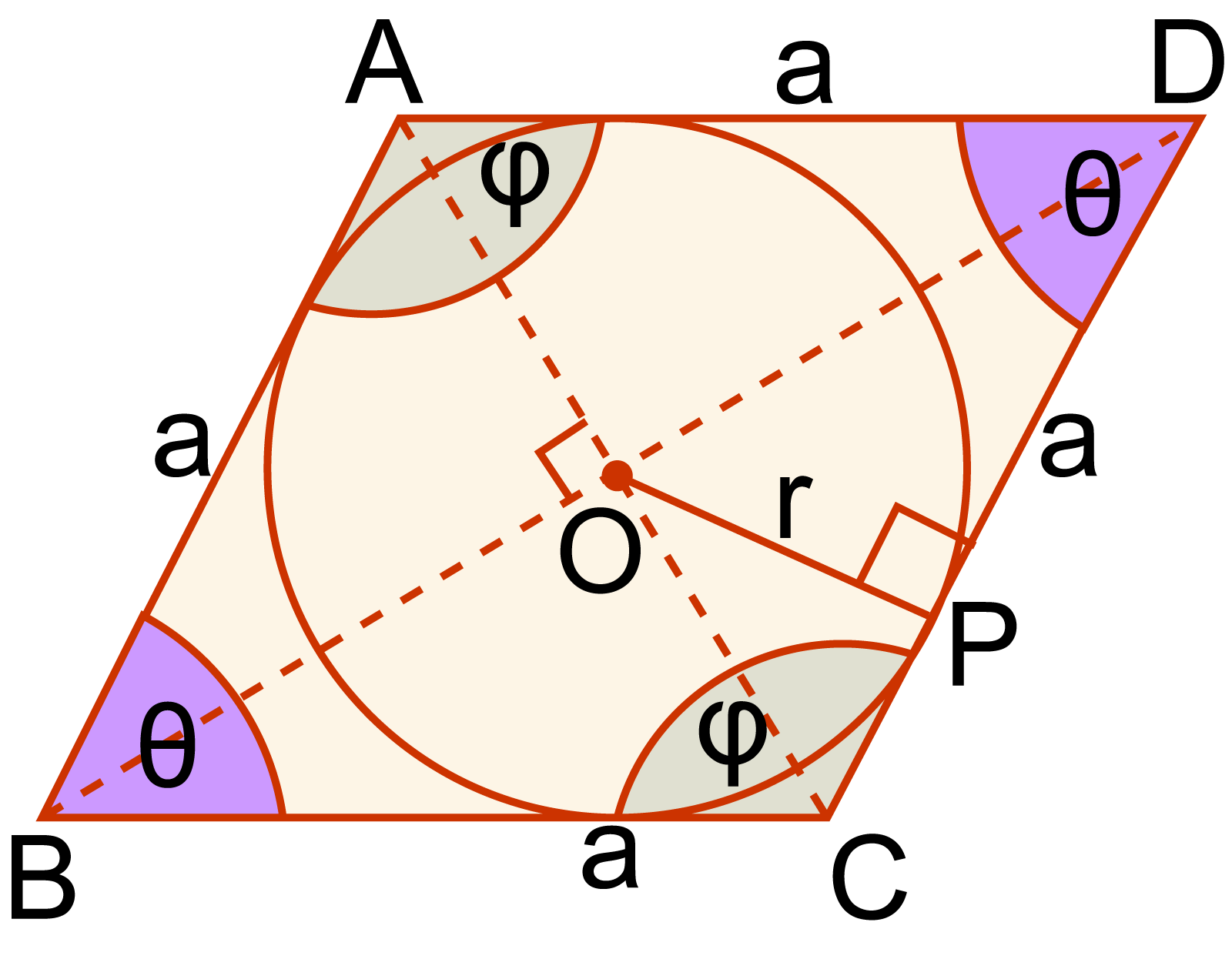
মনে করি, ABCD একটি রম্বস যার বাহুর দৈর্ঘ্য AB = BC = CD = DA = a একক।
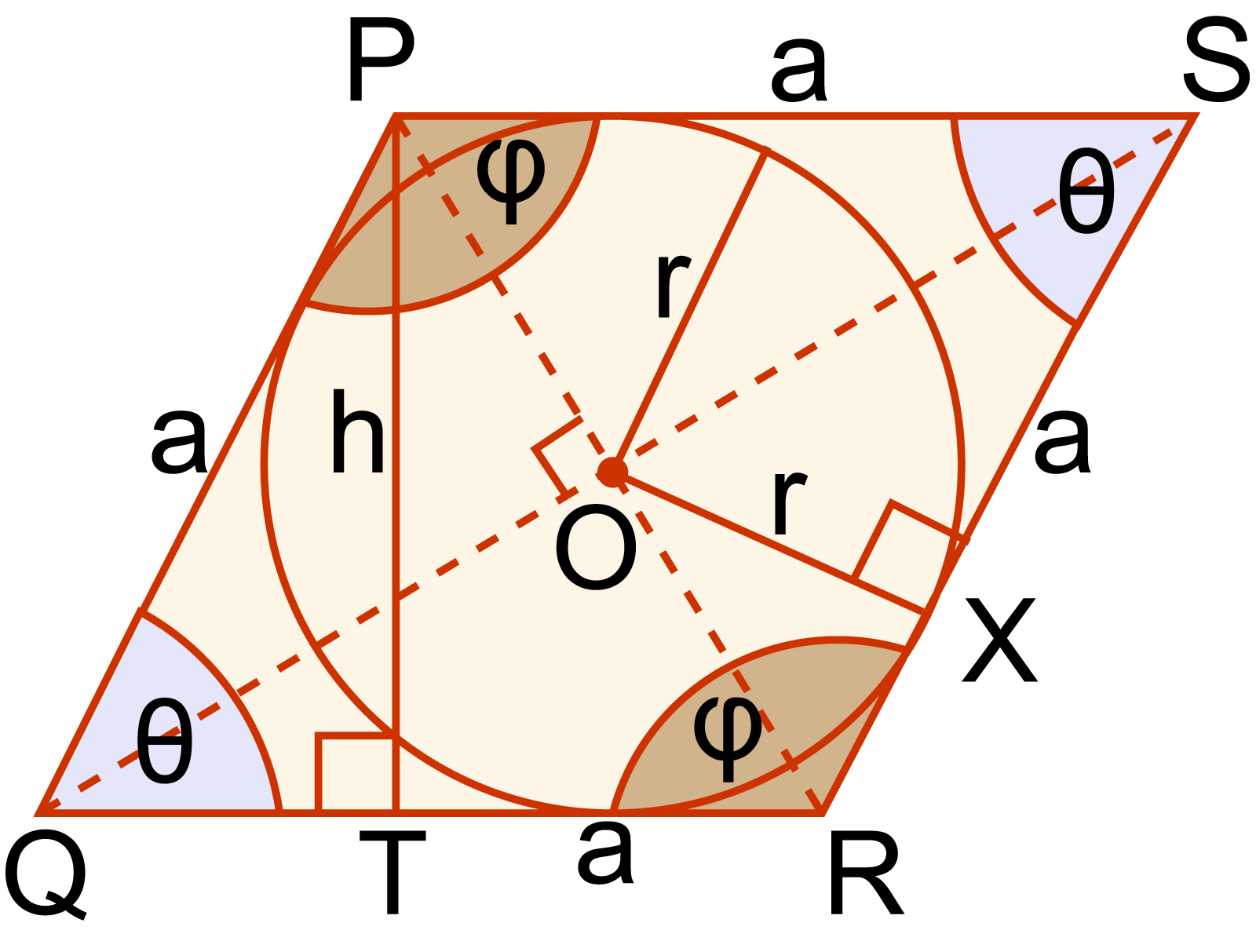
ABCD রম্বসে O কেন্দ্রবিশিষ্ট বৃত্তটি অন্তর্লিখিত; যার ব্যাসার্ধ r একক। OP⊥CD আঁকি যেখানে OP = r.
আবার রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে। AC ও BD কর্ণদ্বয় রম্বসটিকে চারটি ত্রিভুজে বিভক্ত করে।
এখন, △AOB ও △BOC -এ
AB = BC,
OA = OC এবং
OB = OB
∴ △AOB ≅ △BOC
অনুরূপভাবে প্রমাণ করা যায় যে,
△AOB ≅ △AOD ≅ △COD ≅ △BOC
ABCD রম্বসের ক্ষেত্রফল - △AOB, △AOD, △COD ও △BOC ত্রিভুজ চারটির ক্ষেত্রফলের সমষ্টির সমান। অর্থাৎ,
◇ABCD = △AOB + △AOD + △COD + △BOC
বা, ◇ABCD = △COD + △COD + △COD + △COD
বা, ◇ABCD = 4 × △COD
বা, ◇ABCD = 4 × 12 × ভুমি × উচ্চতা
বা, ◇ABCD = 4 × 12 × CD × OP
বা, ◇ABCD = 4 × 12 × a × r
বা, ◇ABCD = 2 × a × r
বা, ◇ABCD = 2a × r
∴ ◇ABCD = পরিসীমা2 × ব্যাসার্ধ
রম্বসের ক্ষেত্রফল =(অর্ধপরিসীমা × ব্যাসার্ধ) বর্গ একক।
অতএব বলা যায়, কোনো রম্বসের অর্ধ-পরিসীমাকে ঐ রম্বসে অন্তর্লিখিত বৃত্তের ব্যাসার্ধ দ্বারা গুণ করলে রম্বসের ক্ষেত্রফল পাওয়া যায়।
রম্বসের বাহুর দৈর্ঘ্য a একক এবং অন্তর্লিখিত বৃত্তের ব্যাসার্ধ r একক হলে,
রম্বসের ক্ষেত্রফল = 2ar বর্গ একক।
রম্বসের ক্ষেত্রফল =(অর্ধপরিসীমা × ব্যাসার্ধ) বর্গ একক।